امروز 29 اردیبهشت رأیگیری برای ریاست جمهوری و شوراهای شهر و روستا برگزار میشود. از اینرو تصمیم گرفتیم یکی از گزارشهای علمی امروز را به بررسی فرایند رأیگیری از دیدگاه علمی اختصاص دهیم. در کنار فضای سیاسی و اجتماعی هر رأیگیری، اساس هر فرآیند به مبانی ریاضی آن برمیگردد. پس بیایید با هم نگاهی به مبانی ریاضی یک سیستم رأیگیری بیندازیم و با یک پرسش موضوع را آغاز کنیم. آیا سیستمی ایدهآل برای رأیگیری وجود دارد که بتواند در همه شرایط خواست اکثریت را بهدرستی بازگو کند؟
فرض کنید بین نه نفر برای خرید بستنی وانیلی و شکلاتی رأیگیری شود و 5 نفر از 9 نفر بستنی شکلاتی را انتخاب کنند؛ بنابراین خواست اکثریت بستنی شکلاتی خواهد بود تا زمانی که تعداد انتخابها دو مورد باشد، مشکل خاصی در تعیین نظر اکثریت وجود ندارد.

فرض کنید انتخاب سومی مانند بستنی توتفرنگی اضافه شود. آنگاه سه حالت برای یک فرد اتفاق میافتد؛ یا بستنی توتفرنگی در ارجحیت سوم و آخر قرار دارد؛ یا در مکان دوم قرار دارد؛ یا ارجحیت اول فرد است که بدین ترتیب انتخاب اولش تغییر میکند و بستنی توتفرنگی میشود.
در مثال قبلی فرض کنید هر پنج نفری که انتخابشان وانیلی بوده و سه نفر از افرادی که انتخابشان شکلاتی بوده است، بستنی توتفرنگی ارجحیت آخر آنها باشد و فقط دو نفر از افرادی که انتخابشان شکلاتی بود، توتفرنگی انتخاب اولشان باشد. در نتیجه رأی خود را به بستنی توتفرنگی تغییر بدهند. اتفاقی که رخ میدهد این است که رأی 5 نفر وانیلی و 3 نفر شکلاتی و 2 نفر توتفرنگی میشود در نتیجه وانیلی بهعنوان خواست اکثریت انتخاب میشود.
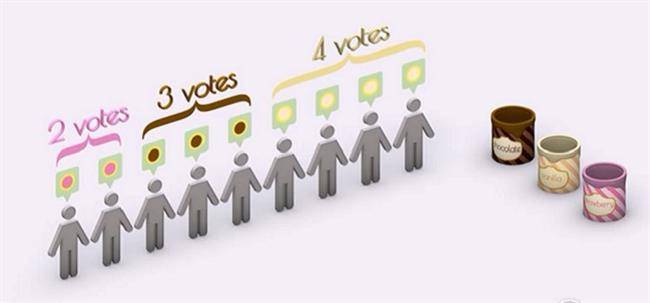
در واقع تأثیر انتخاب سوم بدین گونه است که انتخاب سوم نادیده گرفته میشود و انتخاب گروه از شکلاتی به وانیلی تغییر پیدا میکند؛ درحالیکه میدانیم در این گروه، بستنی شکلاتی به وانیلی ارجحیت دارد و انتخاب شکلاتی اکثریت را خوشحال خواهد کرد. به این پدیده اثر ضایع کننده میگویند. در واقع بستنی توتفرنگی بدون اینکه خود شانس برد داشته باشد، شانس برد دیگری را ضایع کرده است. برای اینکه این پدیده رخ ندهد، ما باید سیستم رأیگیری خود را عوض کنیم. بنابراین از رأیگیری ترجیحی استفاده میکنیم؛ بدین معنی که هر فرد انتخابهای خود را بر اساس اولویت لیست میکند. بنابراین برای مثال قبل داریم:

همانطور که از تصویر میتوان نتیجه گرفت، بین شکلاتی و وانیلی، اولویت با بستنی شکلاتی است. بین وانیلی و توتفرنگی، با وانیلی و در انتها بین شکلاتی و توتفرنگی با شکلاتی است. بنابراین انتخاب گروه به ترتیب شکلاتی، وانیلی و توتفرنگی است و بستنی شکلاتی بهعنوان خواست اکثریت انتخاب خواهد شد. در این مرحله بیایید مثال دیگری را با 12 نفر رأیدهنده، توسط رأیگیری ترجیحی همانند تصویر زیر بررسی کنیم.
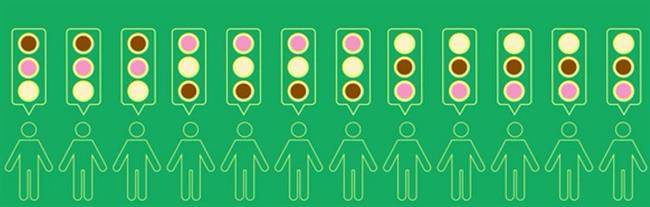
انتخاب اکثریت، شکلاتی نمیتواند باشد؛ چون اکثریت وانیلی را بر شکلاتی ترجیح میدهند. اما از طرف دیگر وانیلی نمیتواند باشد؛ چون اکثریت توتفرنگی را به وانیلی ترجیح میدهند و در نهایت توتفرنگی هم نمیتواند باشد؛ چون اکثریت شکلاتی را به آن ترجیح میدهند. مهم نیست انتخاب اکثریت را چه فرض کنیم؛ همیشه انتخاب دیگری هست که گروه را خوشحالتر کند. به نظر میرسد این گروه انتخاب ارجح ندارد. به این پدیده، ترجیح دوری یا پارادوکس کندورسه گفته میشود. برای اینکه بدانیم مشکل از کجا است، در نظر داشته باشید ترتیب ارجحیت گروه برای سه انتخاب، 6 حالت دارد؛ اما بررسی دوبهدوی سه انتخاب، 8 حالت ممکن دارد که دو حالت آخر در واقع پدیده ترجیح دوری را ایجاد میکنند.
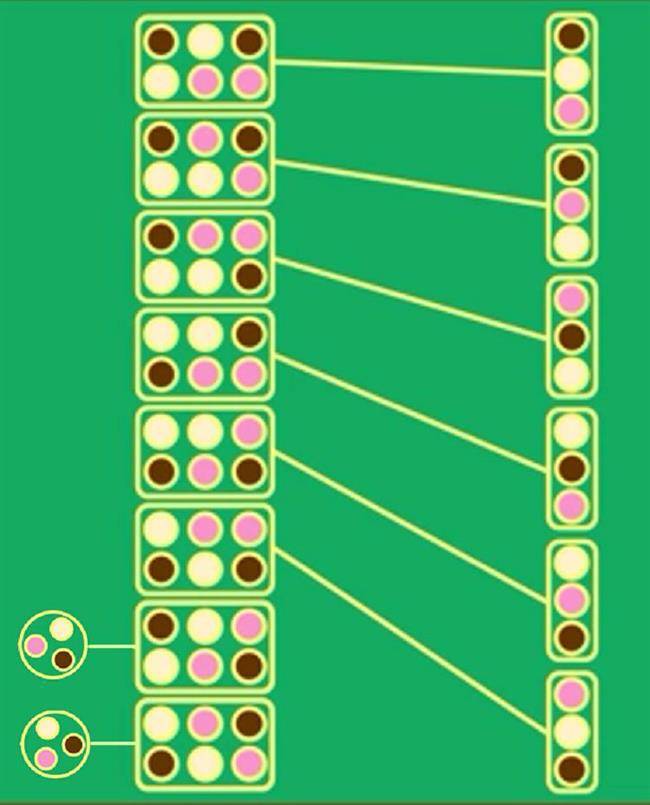
برای رفع این مشکل بیایید از سیستم رأیگیری حذفی استفاده کنیم. بدین صورت که ابتدا انتخابی که کمترین رأی را دارد، حذف میکنیم و سپس بین دو گزینه دیگر بررسی را انجام میدهیم. در این مثال بستنی شکلاتی با سه انتخاب حذف میشود و بین دو انتخاب دیگر بستنی توتفرنگی با نتیجه 7 به 5 برنده خواهد شد. در رأیگیری حذفی، پدیدهی ترجیح دوری اتفاق نمیافتد و اینکه همیشه ارجحیت انتخاب میشود. اما همانند گذشته، سیستم رأیگیری جدید با اینکه مشکلات ما را رفع کرده است، اما دارای ایراداتی بسا عجیبتر هست.
مثالی را با 17 نفر در نظر بگیرید که انتخابهای آنها بهصورت تصویر زیر باشد.

با استفاده از رأیگیری حذفی بستنی وانیلی با 5 انتخاب حذف میشود و بین دو انتخاب دیگر، بستنی شکلاتی با 11 رأی در مقابل 6 رأی از بستنی توتفرنگی میبرد. اما فرض کنید قبل از خرید بستنی، گفته شود اگر انتخاب گروه بستنی شکلاتی باشد به هر فرد یک عدد آبنبات هم داده خواهد شد. با توجه به این گفته فرض کنید دو تا از افرادی که انتخابشان توتفرنگی بود، متقاعد شدند که بستنی شکلاتی را در ارجحیت قرار بدهند.

دقت کنید بستنی شکلاتی از قبل بهعنوان ارجحیت این گروه انتخاب شده بود و عوض شدن انتخاب دو نفر به بستنی شکلاتی در جهت افزایش خواست گروه نسبت به بستنی شکلاتی است؛ اما نتیجهی فرایند رأیگیری متفاوت خواهد بود، این بار بستنی توتفرنگی با 4 انتخاب حذف و بستنی وانیلی با 9 رأی از 17 رأی برنده میشود. در واقع با اینکه انتخاب اول نسبت به بستنی شکلاتی بیشتر شده؛ اما بستنی شکلاتی به علت انتخاب بیش از حد باخته است! به این پدیده شکست یکنواختی گفته میشود.
این یکی از مثالهایی است که نشان میدهند اگرچه ممکن است در یک گروه، هر فرد بهصورت مستقل رفتارهای معقولانهای بروز دهد؛ اما گروه بهعنوان یک کل میتواند رفتاری کاملا عجیب از خود نشان دهد.
به پدیدههای ذکرشده، پارادوکسهای رأیگیری گفته میشود و هر کدام نشان میدهد که انتخابهای گروهی چقدر متفاوت نسبت به انتخابهای فردی میتوانند رفتار کنند. شاید تصور شود که این موارد ایرادات فنی هستند و سیستم رأیگیری ایدهآل وجود دارد که در هر شرایطی عاری از این مشکلات باشد. اما در اوایل دهه 50 میلادی، اقتصاددان آمریکایی کنت ارو نشان داد پارادوکسهایی همانند موارد بالا اجتنابناپذیر هستند. به زبان ریاضی، هیچ سیستم رأیگیری وجود ندارد که ارجحیت فردی را به ارجحیت یک گروه مرتبط کند و عاری از پارادوکسهای رأیگیریِ شناختهشده باشد.
وقتی هر فرد یک رأی میدهد، در راستای انتخاب یک نوع بستنی کمک میکند. اما وقتی یک سیستم رأیگیری را انتخاب میکنیم در واقع از میان پارادوکسهای رأیگیری موجود یکی را انتخاب کردهایم. این موضوع محدودیتهای تصمیمگیری گروهی را نشان میدهد که با عنوان قضیهی عدم امکان ارو شناخته میشود. کنت ارو بعدها به خاطر این نتیجه، برنده نوبل اقتصاد شد. نتیجهای که باعث پیدایش نظریه انتخاب اجتماعی مدرن شد؛ بخشی از ریاضی که چگونگی تصمیمگیری گروهها را بررسی میکند.
رأیگیری یکی از ارکان جداییناپذیر زندگی اجتماعی مدرن است؛ اما عدم وجود یک سیستم رأیگیری ایدهآل شاید یکی از دیگر مواردی است که عدم وجود یک دنیای ایدهآل را نشان میدهد. نظر شما در این مورد چیست؟