اگر بتوانید پیش‌بینی خوبی از پاسخ رقبا به اقدامات خود داشته باشید، چه خواهد شد؟

اگر بتوانید قبل از هر اقدامی پیش‌بینی خود را از عکس‌العمل رقبا در تصمیمات خود لحاظ کنید چه اثری بر دستیابی شما به منافع‌تان خواهد گذاشت؟ و بهتر از اینها، اگر این کار را به جای اینکه با حدس‌های خود انجام دهید، با تکیه بر یک روش علمی انجام دهید، چه نتیجه‌ای را در پی خواهد داشت؟

شناسایی و درک اینکه دیگران نسبت به تصمیمات شما چه واکنشی نشان خواهند داد، یکی از مهمترین موارد در بسیاری از حوزه‌های کسب‌وکار است.

به عنوان مثال، تصور کنید با چند شرکت دیگر در حال رقابت در یک بازار هستید. اگر بتوانید حرکات آنها را پیش‌بینی کنید، قادر خواهید بود برخی از انتخاب‌های آنها را از میان بردارید یا اینکه وقتی اقدامی انجام دادند بتوانید با اقدامی متقابل و متناسب، در مقابل آنها پیروز شوید. نظریه بازی‌ ها ابزار لازم برای تفکر پیرامون این مسائل را به شما می‌دهد.

نظریه بازی‌ ها چیست؟

نظریه بازی‌ ها، تلاشی مستدل جهت پیش بینی رفتار دیگران است. از این نظریه‌ می‌توان در مواقعی استفاده کرد که موفقیت فرد در تصمیم گیری به تصمیمات دیگران بستگی دارد. مدل ساده‌ای از این نظریه شامل این عناصر می‌شود:

• بازیکنان
• مجموعه‌ای از اقداماتی (تصمیماتی) که بازیکنان می‌توانند انتخاب کنند
• بهایی که هر بازیکن بابت باختن می‌پردازد و یا پاداشی که بابت برنده شدن به دست می‌آورد

جان فون نیومن (John von Neumann) و اسکار مانگسترن (Oskar Morgenstern) اصول نظریه بازی‌ ها را در سال 1994 در کتاب خود تحت عنوان «نظریه بازی‌ ها و رفتار اقتصادی» منتشر کردند.

بازی‌های همزمان و متوالی

موقعیت‌های توصیف شده توسط نظریه بازی‌ ها به دو دسته‌ی اصلی تقسیم می‌شوند:

• بازی‌های حرکت هم‌زمان: در این دسته، بازیکنان هم‌زمان با هم حرکات خود را انجام می‌دهند؛ مثل بازی سنگ کاغذ قیچی، یا مواقعی که شرکت‌هایی که با هم رقابت دارند، محصول جدید خود را با شروع سال جدید هم‌زمان با هم روانه‌ی بازار می‌کنند.
• بازی‌های حرکت متوالی: در این بازی‌ها، بازیکنان به صورت نوبتی بازی می‌کنند. مثل شطرنج، یا مواقعی که دو شرکتی که با هم رقابت دارند به صورت نوبتی به تغییر قیمت محصولات یکدیگر واکنش نشان می‌دهند.

بازی‌های حرکت هم‌زمان

ابتدا بازی‌های حرکت هم‌زمان را مورد بررسی قرار می دهیم.

در بازی‌های حرکت هم‌زمان، برای اینکه بازیکنان بفهمند که چه اقدامی را انتخاب کنند، باید قبل از اینکه بازی را شروع کنند، در ذهن خود جدولی را تنظیم کنند که به آن «جدول نتیجه‌ی نهایی» گفته می‌شود. این جدول، عواقب و نتایج حرکت‌های مختلفی را که بازیگران در بازی می‌توانند انتخاب کنند؛ به صورت کمی نشان می‌دهد. مثال زیر ساده‌ترین حالت را نشان می‌دهد که دو بازیگر وجود دارد که هر کدام فقط می‌توانند یک حرکت داشته باشند و فقط دو انتخاب برای حرکت خود دارند. در نتیجه چهار خروجیِ ممکن به صورت زیر قابل تصور است:

1. هر دو بازیکن حرکت «الف» را انجام بدهند.
2. بازیکن 1 حرکت «الف» و بازیکن 2 حرکت «ب» را انجام بدهد.
3. بازیکن 1 حرکت «ب» و بازیکن 2 حرکت «الف» را انجام بدهد.
4. هر دو بازیکن حرکت «ب» را انجام بدهند.

این موقعیت را می‌توان در مثالی از دو شرکت تولیدکننده به کار برد که تنها شرکت‌هایی هستند که در یک بازار مشغول فعالیت و رقابت با هم هستند. هر کدام از آنها در حال حاضر 50 درصد از سهم بازار را در اختیار دارند و سالانه فروشی معادل 2 میلیارد تومان دارند.

با پیشرفت فناوری برای هریک از آنها شرایطی فراهم شده تا نسل بعدی محصول تولیدی خود را تولید و روانه‌ی بازار کنند؛ اما این کار 500 میلیون تومان هزینه در پی خواهد داشت.

اگر هردو شرکت اقدام به عرضه‌ی محصول جدید کنند، بازار کلی 10 درصد رشد خواهد داشت و تعداد مشتریان فعلی با افزایش روبه‌رو خواهد شد.

اگر فقط یکی از شرکت‌ها محصول جدید را ارائه کند، سهم بازار آن شرکت به 75 درصد افزایش می‌یابد، اما بازار کلی 5 درصد افزایش خواهد داشت. زیرا برخی از مشتریان به تولید کننده‌ای که محصول جدید را تولید نکرده وفادار باقی خواهند ماند.

اگر هیچ کدام از شرکت‌ها به تولید و عرضه‌ی محصول جدید نپردازند، فروش بدون تغییر باقی خواهد ماند.

جدول نتیجه‌ی نهایی برای این مثال که در زیر آمده است، درآمد حاصل از فروش مورد انتظار در سال اول برای چهار حالت ممکن را برای هر بازیگر نشان می‌دهد. (اعداد بالا در هر خانه نتایج مربوط به شرکت 1 و اعداد پایین نتایج شرکت 2 را نشان می‌دهند)

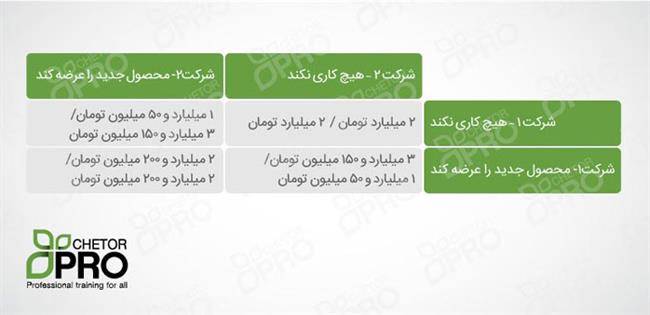
هزینه‌ی تولید و عرضه‌ی محصول جدید نیز باید محاسبه شود، لذا جدول فوق با کسر هزینه‌ها از درآمد حاصل از فروش به صورت زیر تغییر می‌کند:

حال سؤال اینجاست که این دو شرکت باید چه کار کنند؟

مشخص است که بهترین خروجی برای هر شرکت این است که خودش محصول جدید را تولید و عرضه کند و رقیبش این کار را انجام ندهد. اما هیچ‌کدام نمی‌دانند که رقیب چه کار خواهد کرد.

اگر هر دو شرکت هیچ کاری در مورد محصول جدید انجام ندهند، این ریسک وجود دارد که هر لحظه شرکت مقابل دست به تولید محصول جدید بزند و درآمد شرکت تا 50 درصد کاهش یابد. از سوی دیگر اگر یک شرکت دست به تولید محصول جدید بزند و رقیب آن کاری نکند، شرایطی بسیار عالی خواهد داشت و چنانچه پس از مدتی شرکت رقیب نیز وارد تولید محصول جدید شود، کاهش درآمد حاصل از ورود رقیب به بازار چشمگیر نخواهد بود.

انتخاب درست این است که شرکت پا پیش بگذارد و دست به تولید محصول جدید بزند، اما در این صورت، مدیران باید مراقب باشند و خود را برای جنبه‌های منفی‌ای که ممکن است با ورود رقیب به وقوع بپیوندند آماده کنند. (در حقیقت، اگر دو طرف موقعیت پیش آمده را به شکلی منطقی تحلیل کنند، احتمالا هر دو طرف، دست به تولید محصول جدید خواهند زد و مقداری کاهش در درآمد سالیانه‌ی خود را متقبل می‌شوند.)

معمای زندانی

بازی معمای زندانی یک مثال کلاسیک برای نظریه بازی‌ ها است. دو زندانی در یک پرونده‌ی سرقت به عنوان متهمین شریک در جرم دستگیر شده‌اند و به هردو پیشنهادهای زیر داده شده است:

• اگر هیچ یک از زندانی‌ها به سرقت اعتراف نکند، هردو برای یک سال به زندان خواهند رفت.
• اگر یکی از زندانی‌ها اعتراف کند و بپذیرد که علیه دیگری شهادت دهد، ولی زندانی دیگر اعتراف نکند، آن زندانی که اعتراف کرده آزاد می‌شود و آن یکی 5 سال به زندان خواهد رفت.
• اگر هر دو اعتراف کنند، برای هر یک از آنها سه سال حکم زندان صادر خواهد شد.

برای بازی‌های حرکت همزمان عموماً می‌توانیم یک جدول نتیجه‌ی نهایی تنظیم کنیم که ترکیب‌های مختلفی از انتخاب‌های ممکن را نشان دهد. این جدول برای مثال زندانی‌ها در زیر نشان داده شده است. ( 1 ، به معنی یکسال حکم زندان است و بقیه اعداد هم به همین شکل)

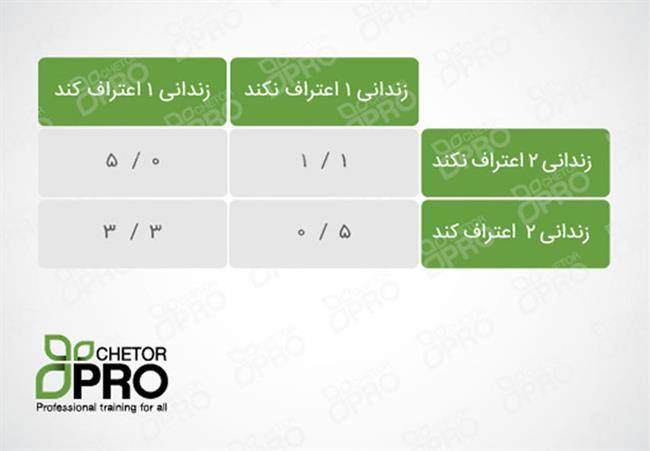
در تئوری، بهترین انتخاب مشترک دو زندانی این است که هیچ یک اعتراف نکنند و هر کدام یک سال به زندان بروند. اما مسئله اینجاست که هیچ کدام مطمئن نیستند که آن یکی اعتراف نکند (چرا که اگر اعتراف کند ممکن است کلاً آزاد شود)، پس هر دو زندانی اعتراف می‌کنند و به جای اینکه هر کدام فقط یک سال به زندان بروند، حکم سه سال زندان برای آنها صادر می‌شود.

بازی‌های حرکت متوالی و درخت بازی

برای بازی‌های حرکت متوالی که در آن هر یک از بازیکنان باید در نوبت خود و یکی پس از دیگری حرکت‌شان را انجام بدهند، به جای جدول نتیجه‌ی نهایی از «درخت بازی» استفاده می‌کنیم. درخت بازی از یک نقطه‌ی منفرد شروع می‌شود و سپس با توجه به حرکت‌های ممکن توسط بازیکن اول شاخه‌ای از نقطه‌ی شروع منشعب خواهد شد. سپس از هر شاخه‌ی جدید با توجه به انتخاب‌های ممکن شاخه‌های دیگری منشعب می‌شود تا جایی که همه‌ی انتخاب‌های ممکن توسط بازیکن دوم پوشش داده شود و به همین ترتیب تا آخر.

بیشتر مذاکرات به عنوان بازی‌های حرکت متوالی به حساب می‌آیند و می‌توانید آنها را با استفاده از درخت بازی مدل کنید. به عنوان مثال، فرض کنید یک فست فود می‌خواهد یک خودرو برای تحویل سفارشاتش تهیه کند. صاحب فست فود با یک فروشنده خودرو آشنا می‌شود که خودرویی متناسب با نیازهای او را با قیمت 30 میلیون تومان به او پیشنهاد می‌دهد. در این حالت سه انتخاب برای او وجود دارد: قبول پیشنهاد، رد کردن پیشنهاد یا درخواست تخفیف. اگر رد کردن پیشنهاد را انتخاب کند ممکن است فروشنده مذاکره را ترک کند یا قیمت مناسب‌تری پیشنهاد دهد. اگر در خواست تخفیف کند، ممکن است تخفیف بدهد یا مذاکره را ترک کند؛ به همین شکل تا آخر.

شکل زیر یک نمونه درخت بازی را برای این مذاکره نشان می‌دهد.

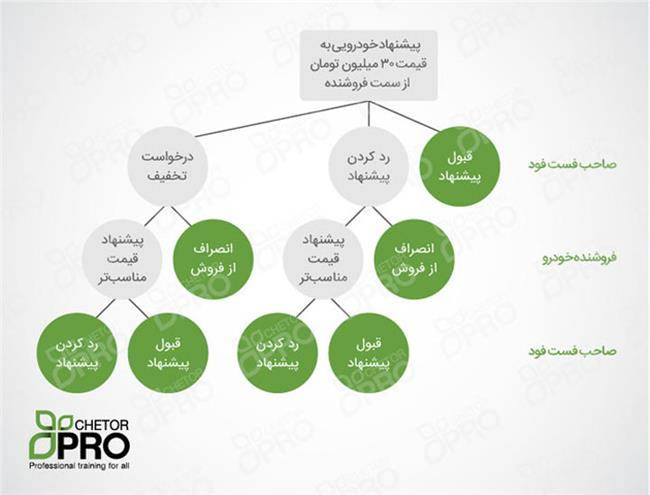
برخلاف این مثال ساده، درخت بازی ممکن است به سرعت پیچیده و بزرگ شود.

استدلال عقب گرد

درخت بازی که برای تشریح بازی‌های حرکت متوالی استفاده می‌شود به شما این امکان را نیز خواهد داد تا با نگاهی به آینده به عقب برگشته و با توجه به یافته‌های خود استدلال کنید که چه تصمیماتی درست هستند. این موضوع به شما اجازه خواهد داد تا دریابید که برای اینکه در آینده بیشترین احتمال برای دستیابی به موفقیت را داشته باشید، استراتژی امروز شما باید به چه صورت باشد. این روش به نام «استقرای عقب گرد» (backward induction) نیز شناخته شده است.

برای پی بردن به اینکه بازی چگونه پیش خواهد رفت از انتهای درخت شروع کنید، با این فرض که رقیب شما بهترین تصمیمات را گرفته و بهترین حرکت ممکن را انجام خواهد داد. همین طور که درخت را مورد بررسی قرار می‌دهید آن شاخه‌هایی را که فکر می‌کنید بیانگر انتخاب‌هایی هستند که منجر به شکست خواهند شد را حذف (هرس) کنید. آنچه که در انتها می‌ماند محتمل‌ترین خروجی بازی است، با این فرض که هیچ یک از دو طرف در حین بازی مرتکب اشتباهی نخواهد شد.

به مثال ساده‌ی بالا نگاه کنید. صاحب فست فود باید درخواست تخفیف بدهد، فروشنده احتمالا آن را قبول می‌کند و در نهایت صاحب فست فود معامله را می‌پذیرد. در غیر این صورت فروشنده نمی‌تواند خودروی خود را بفروشد و صاحب فست فود هم نمی‌تواند این خودرو را برای تحویل سفارشات تهیه کند. (البته با این فرض که به فروش این خودرو احتیاج دارد و صاحب فست فود نیز پیشنهاد بهتری دریافت نخواهد کرد.)

وقتی که بازی به یک نقطه‌ی تعادل می‌رسد…

در بسیاری از مواقع، بازی به یک حالت پایدار می‌رسد که در نظریه بازی‌ ها به آن «تعادل نش» می‌گویند. (به یاد جان نش John Nash، یکی از نظریه پردازان این حوزه، نامگذاری شده است.) در چنین موقعیتی بازیکنان از استراتژی‌های یکدیگر آگاه هستند و هرکدام بهترین تصمیم را در شرایط خاص خود می‌گیرند. وقتی که آنها حرکات خود را انجام دادند، هیچ کدام از طرفین تمایلی به تغییر استراتژی خود نشان نمی‌دهد.

مثال آن در کسب‌وکار می‌تواند زمانی باشد که شرکت‌های فعال در یک بازار به دنبال حداکثر کردن سود خود با انتخاب سطح مشخصی از خروجی هستند. بهترین خروجی (و سود) برای یک شرکت به خروجی‌های شرکت‌های دیگر بستگی دارد. پس هر حرکتی از یک شرکت بستگی به حرکت شرکت دیگر دارد و این شرایط با تکرار حرکت‌های طرفین به حالت پایدار درمی‌آید و به نقطه‌ی تعادل نش خواهیم رسید.

نظریه بازی‌ ها در زندگی واقعی

نظریه بازی‌ ها در زندگی واقعی به عوامل متعددی بستگی دارد. حتی اگر از فرمول‌های ریاضی برای محاسبه‌ی خروجی‌های بازی استفاده شود در زندگی واقعی به یک حس مشترک و درک این حس نیاز است. به عنوان نمونه در مثال معمای زندانی، ممکن است این دو زندانی چند سال بعد دوباره خود را در یک شرایط مشابه در دادگاهی برای پرونده‌ی سرقت ببینند. با توجه به شیوه‌ای که بار اول به آن عمل کرده‌اند، احتمال این که این دفعه چگونه عمل کنند تغییر خواهد کرد، به ویژه اگر این دفعه بخواهند تلاش کنند که اشتباهاتی که دفعه‌ی قبل انجام داده‌اند را تکرار نکنند.

به همین ترتیب، در تفکر درباره‌ی کسب‌وکارها، به عنوان مثال صنعت حمل و نقل هوایی، می‌توانیم از مدل‌های مختلفی استفاده کنیم. اما این مدل‌ها نسبت به تغییرات قیمت و عکس العمل‌های رقابتی میان شرکت‌های هواپیمایی محدودیت دارند. در چنین مواقعی می‌توانیم احتمالات اضافه‌ی دیگری را نیز با استفاده از نظریه بازی‌ ها مدل کنیم؛ احتمالاتی نظیر ورود شرکت‌های هواپیمایی جدید به بازار (با قیمت‌های پایین‌تر)، تغییر تصمیم مشتریان برای انتخاب روش سفر (استفاده از قطار و …) و یا فعالیت‌های ضدرقابتی و استفاده از تاکتیک‌های جنگ قیمتی توسط شرکت‌های هواپیمایی.