هر ساله، چهاردهمین روز از سومین ماه میلادی (3.14) را می توان روز مقدس ریاضیدانان دانست که به صورت نمادین به بزرگداشت یکی از اسرارآمیزترین مفاهیم ریاضی به نام «عدد پی» می پردازند. البته بعضی ها به رسم وفاداری، عدد پی را تا چهار رقم اعشار (3.1415) حساب کرده و جشن خود را تا پانزدهم مارس نیز ادامه می دهند.
عدد پی تا 31 رقم اعشار برابر است با 3.1415926535897932384626433832795 و البته این زنجیره هیچگاه به پایان نمی رسد، یا تکرار نخواهد شد.
عدد پی چیست؟
پی از تقسیم محیط یک دایره به قطر آن به دست می آید و از آنجا که با نسبت هیچ دو عدد کاملی برابر نیست، معمولاً به صورت تقریبی آن را برابر با حاصل تقسیم 22 بر 7 در نظر می گیرند. عدد پی در معماری و مهندسی از اهمیت بسزایی برخوردار است و اخترشناسان نیز دائماً از آن استفاده می کنند. کشف این عدد به حدود 4000 سال قبل بر می گردد، اما از اواسط سده 1700 میلادی به آن Pi می گویند.
پس از گذشت هزاران سال فعالیت مستمر، ریاضیدانان هنوز در تلاشند تا پرده از اسرار عدد پی بردارند. ما معمولاً پی را به صورت تقریبی و برابر با 3.14 در نظر می گیریم، اما محاسبات سنگین کامپیوتری توانسته اند مقدار آن را تا 13 تریلیون رقم اعشار به دست آورند.
تقریباً از قرن هجدهم میلادی، دانشمندان به این باور رسیدند که هیچگاه نمی توان تمام ارقام عدد پی را محاسبه کرد، چون پی یک «عدد گنگ» است، یعنی بدون هیچگونه تکرار در الگوی اعداد، تا بی نهایت ادامه خواهد یافت.
در سال 1881 «جان وِن» فیلسوف و منطق دان بریتانیایی که «نمودار وِن» را نیز ابداع کرد، تمام تلاش خود را به کار گرفت تا به صورت بصری نشان دهد ارقام عدد پی تصادفی هستند. او گرافی را ترسیم کرد که 707 رقم اعشار پی را نشان می داد و برای تصویرسازی، به هرکدام از ارقام صفر تا 7 یک جهت جغرافیایی را نسبت داد. این نمودار که به Pi Walk معروف است را در زیر می بینید:
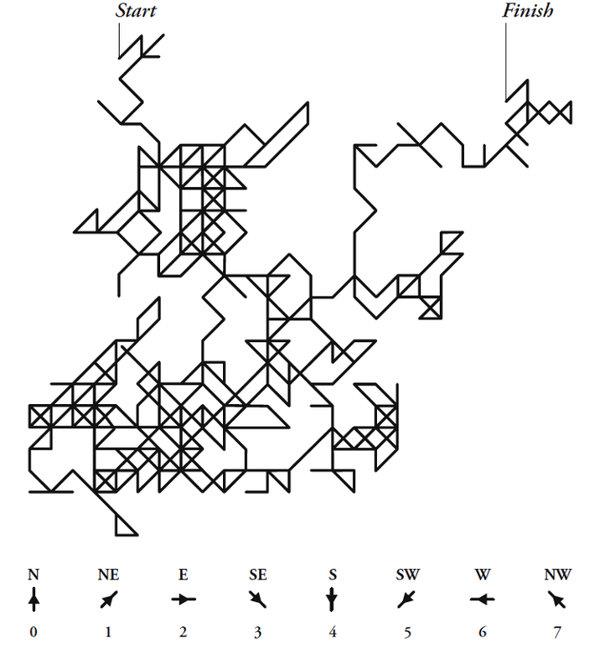
اگرچه وِن تصویر فوق را با قلم و کاغذ ترسیم کرد، اما محققین و علاقه مندان در حال حاضر با استفاده از تکنولوژی های نوین به گشت و گذار در دنیای بیکران عدد پی می پردازند و الگوهای عجیب و زیبایی را به ثبت می رسانند. به عناون مثال تصویر زیر پیمایش تصادفی عدد پی را تا 100 میلیارد رقم نشان می دهد:

با این حال، علی رغم اینکه با رشته ای بی پایان از ارقام غیر قابل پیش بینی در عدد پی روبرو هستیم، اما نمی توان آن را «تصادفی» خواند، ضمن اینکه هر از گاهی الگوهای کاملاً غیرمنتظره و هیجان انگیز در این دنباله مشاهده می شود.
نرمال، نه تصادفی
دلیل اینکه نمی توان پی را تصادفی خواند، این است که ارقام تشکیل دهنده آن ثابت و مشخص هستند. مثلاً دومین رقم اعشاری آن همیشه برابر 4 است، و نمی توان احتمالی برای حضور رقم دیگری در این جایگاه را متصور شد. جایگاه ارقام پی به هیچ وجه تصادفی نیست.
حال این سؤال به وجود می آید که «آیا عدد پی نرمال است؟» در تعاریف ریاضی، یک عدد اعشاری را نرمال می گویند اگر احتمال وجود هر دنباله ای از ارقام در آن وجود داشته باشد، اما با این تعریف، عدد حاصل تصادفی به نظر می رسد، حتی اگر به لحاظ فنی اینگونه نباشد.
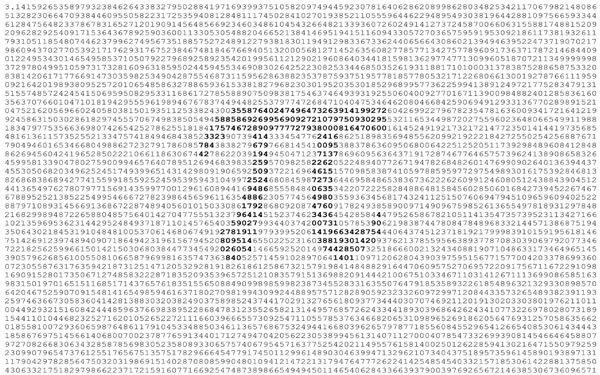
با نگاه به ارقام عدد پی و انجام آزمون های آماری می توانیم نرمال بودن آن را بررسی کنیم، اما با وجود تلاش های متعددی که تاکنون صورت گرفته، هنوز پاسخی برای این سؤال نداریم. به عنوان مثال در سال 2003 «یاسوماسا کانادا» نحوه توزیع ارقام مختلف در یک تریلیون رقم اعشار عدد پی را به صورت زیر محاسبه کرد:
- رقم صفر : 99999458134 تکرار
- رقم یک: 99999945664 تکرار
- رقم دو: 100000480057 تکرار
- رقم سه: 99999787805 تکرار
- رقم چهار: 100000357857 تکرار
- رقم پنج: 99999671008 تکرار
- رقم شش: 99999807503 تکرار
- رقم هفت: 99999818723 تکرار
- رقم هشت: 100000791469 تکرار
- رقم نه: 99999854780 تکرار
- مجموع: 1000000000000 رقم
این نتایج به خوبی نشان می دهند که توزیع ارقام تا یک تریلیون اعشار نسبتاً یکنواخت است، اما باز هم برای اثبات نرمال بودن عدد پی کفایت نمی کند.
حضور هر دنباله ای از ارقام
به خاطر داشته باشید که اگر عدد پی نرمال باشد، آنگاه هر توالی متناهی از ارقام که بخواهید را باید در آن پیدا کنید. مثلاً در موقعیت 768 از ارقام اعشاری پی، شش عدد 9 پشت سر هم قرار گرفته و توالی 999999 را تشکیل داده اند. اگر پی عددی نرمال باشد و دنباله های مختلف اعداد با احتمال برابر در آن حضور داشته باشند، آنگاه احتمال مشاهده 999999 برابر 0.08 درصد است.

این بلوک شش تایی از رقم 9 را به پاس تلاش های ارزشمند «ریچارد فاینمن» فیزیکدان سرشناس آمریکایی و برنده جایزه نوبل، «نقطه فاینمن» نامیدند. او در جریان یکی از سخنرانی هایش به شوخی گفت اگر بخواهد عدد پی را به خاطر بسپارد، تا 762 رقم را حفظ می کند و پس از آن می گوید «9، و الی آخر».
توالی های جالب دیگری نیز در عدد پی وجود دارند، که البته یافتن آنها کار دشواریست. مثلاً پس از اینکه 17 میلیارد و 387 میلیون و 594 هزار و 880 رقم اعشار را پشت سر بگذارید، به دنباله 0123456789 می رسید، و جالب اینکه همین ارقام به صورت متوالی اما در هم ریخته، در موقعیت 60 نیز دیده می شوند.

یکی از سرگرمی های جالب ریاضیدانان و علاقه مندان، یافتن تاریخ تولد خود و دیگر رخدادهای مهم در عدد پی است. شاید برای شما نیز این سؤال جالب باشد: «من کجای عدد پی قرار دارم؟» اگر می خواهید عددهای خاص خودتان را در پی بیابید، می توانید به نرم افزارهای آنلاین مخصوص این کار با نام Pi birthdays مراجعه کنید (لینک نمونه).